TEMA 5: ALTIMETRÍA, CURVAS DE NIVEL Y VOLÚMENES

Perfil altimétrico de una carretera.

ALTIMETRÍA, CURVAS DE NIVEL Y VOLÚMENES

La altimetría (también llamada hipsometría) es la rama de la topografía que estudia el conjunto de métodos y procedimientos para determinar y representar la altura o "cota" de cada punto respecto de un plano de referencia. Con la altimetría se consigue representar el relieve del terreno, (planos de curvas de nivel, perfiles, etc.).

DEFINICIÓN

Se denomina altimetría a la rama de la topografía especializada en la medición de la altura.   Cabe recordar que la topografía es la disciplina que se encarga de la descripción detallada   de las superficies.

Altimetría: También conocida como hipsometría, la altimetría abarca diversos procesos, metodologías y técnicas para la determinación y la representación de la altura de un punto, teniendo en cuenta un cierto plano de referencia. De esta manera, la altimetría posibilita la representación del relieve.

El instrumento que permite conocer la distancia en altura que existe entre un punto y el       plano de referencia se conoce como altímetro. Gracias a este instrumento, se puede        descubrir a qué altura se encuentra un punto respecto al nivel del mar.

La altimetría, de este modo, se hace presente en la aviación. El altímetro está entre los instrumentos de vuelo más importantes, ya que mide de forma constante a qué altura            vuela una aeronave. Para ofrecer este dato, la herramienta calcula la distancia que existe,           en sentido vertical, entre la aeronave y el nivel del mar.

Esto hace que la altimetría sea clave para la aviación ya que las rutas de vuelo se organizan  según la altitud. Una aeronave, por lo tanto, tiene que volar a una determinada altura de  acuerdo a la ruta que se le asigna al piloto; dicho dato surge del altímetro.

DEFINICIÓN DECURVA DE NIVEL

La idea de curva de nivel se emplea en el ámbito de la topografía con referencia a la línea que se forma por aquellos puntos del terreno que se sitúan a la misma altura.        Cabe recordar que la topografía es la disciplina centrada en la descripción y el          delineamiento de la superficie de un terreno.

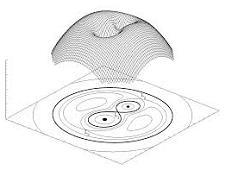
Una curva de nivel, por lo tanto, es la línea que une los puntos de un mapa que tienen idéntica altitud. Por lo general estas líneas aparecen dibujadas en color azul para reflejar las profundidades del océano y los glaciares, y en tonalidad siena con sombreados para marcar la altura del terreno.

La geodesia también recurre a las curvas de nivel. Esta ciencia construye mapas a partir         de la determinación de la magnitud y la figura de regiones del globo terráqueo. Las curvas         de nivel, en este marco, reflejan la representación de una sección horizontal del  relieve. La diferencia existente en la altitud de dos curvas de nivel sucesivas resulta        constante y está vinculada a la escala empleada en el mapa.

Para lograr la representación de las curvas de nivel, lo que se hace es obtener planos        paralelos entre sí mediante cortes en la superficie del terreno. Estos planos se encuentran alejados a una determinada distancia unos de otros. La curva de nivel es la figura formada       por cada uno de estos planos que corta el terreno. Cuando las curvas de nivel, coloreadas           de distinta manera, se proyectan sobre el mapa, se produce la representación.

Curvas de nivel

El sistema de representación de curvas de nivel consiste en cortar la superficie del           terreno mediante un conjunto de planos paralelos entre sí, separados una cierta distancia      unos de otros. Cada plano corta al terreno formando una figura (plana) que recibe el        nombre de curva de nivel o isohipsa. La proyección de todas estas curvas de nivel           sobre un plano común (el mapa) da lugar a la representación buscada.

En la figura se ve la construcción para representar mediante curvas de nivel una           montaña. La montaña es cortada  mediante planos paralelos separados una cierta        distancia que se llama equidistancia entre curvas de nivel.

Curvas de nivel

El sistema de representación de curvas de nivel consiste en cortar la superficie del terreno mediante un conjunto de planos paralelos entre sí, separados una cierta distancia unos de otros. Cada plano corta al terreno formando una figura (plana) que recibe el nombre de curva de nivel o isohipsa. La proyección de todas estas curvas de nivel  sobre un plano común (el mapa) da lugar a la representación buscada.

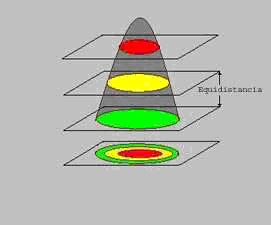
En la figura se ve la construcción para representar mediante curvas de nivel una montaña. La montaña es cortada  mediante planos paralelos separados una cierta distancia que se llama equidistancia entre curvas de nivel.

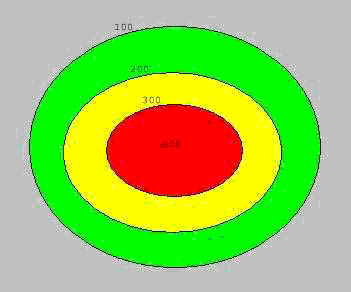
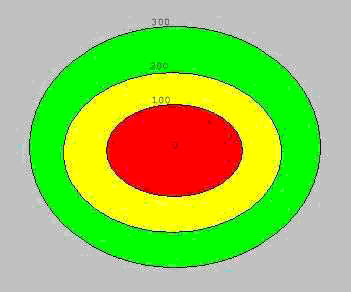
Al observar la figura nos puede quedar la duda sobre qué secciones están por encima de otras. Es decir, ¿está realmente la sección roja por encima de la amarilla y de la verde?

El problema anterior se resuelve fácilmente si para cada sección indicamos su altura con respecto a un plano de referencia, y como tal plano se toma el nivel del mar. De este modo la sección verde se ha obtenido cortando la  montaña mediante un plano paralelo al nivel del mar y una altura (o nivel) de 100 metros con respecto a aquél. La  sección amarilla se ha obtenido mediante la intersección con un plano a 200 metros sobre el nivel del mar (s.n.m.). Y la sección roja con un plano a 300 metros s.n.m. Para cada curva de nivel indicaremos esa altitud y le denominaremos cota.

La equidistancia entre curvas de nivel se puede deducir ahora con facilidad para el ejemplo dado: 100 metros.

En la siguiente figura se ve como se efectúa la construcción de curvas de nivel de una depresión, que es el caso opuesto al monte de la figura anterior.

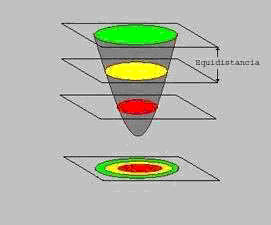
Puede observarse que el procedimiento a seguir es exactamente el mismo y que se obtiene la misma representación.

Sin embargo, la acotación de las curvas de nivel no dejan lugar a dudas. Podemos observar que las curvas de mayor cota encierran a las curvas de cota menor, señal inequívoca de una depresión en el terreno. En un monte ocurre justo lo contrario, las curvas de nivel de menor cota encierran a las de cota mayor.

Las curvas de nivel verifican las siguientes premisas de manera general:

• Las curvas de nivel no se cortan ni se cruzan (sólo ocurre ésto cuando queremos representar una cueva o un saliente de roca).
• Las curvas de nivel se acumulan en las laderas más abruptas y están más espaciadas en las laderas más suaves.
• La línea de máxima pendiente entre dos curvas de nivel es aquella que las une mediante la distancia más corta.

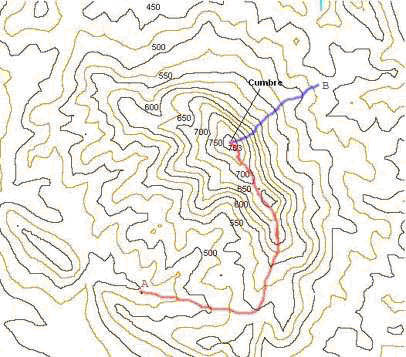
En la siguiente figura tenemos dos itinerarios para alcanzar una cumbre desde dos puntos A y B. Desde el punto A (itinerario rojo) es más largo que desde el punto B (recorrido azul). Sin embargo, el itinerario azul es mucho más duro ya que las curvas de nivel se hallan más apretadas o, si se prefiere, el camino atraviesa las curvas de nivel en menos espacio.

Equidistancia entre curvas de nivel

La distancia entre los diversos planos imaginarios que cortan el terreno es siempre la misma para un mapa dado y se llama equidistancia entre curvas de nivel.

En el plano anterior la equidistancia entre curvas de nivel es de 25 metros. Obsérvese que se usan dos colores para  poder contar mejor las curvas de nivel. Así las líneas más oscuras aparecen cada 50 metros, y entre dos de ellas consecutivas aparece una línea más clara. En cualquier caso entre dos curvas de nivel tendremos una diferencia de  altitud de 25 metros. A las líneas más oscuras se les suele llamar curvas de nivel maestras.

Cota de un punto

Cada punto de un mapa se sitúa a una altitud definida que se viene a denominar cota. La cota de un punto es la longitud vertical que lo separa del plano de comparación, normalmente el nivel del mar.

BIBLIOGRÁFICA:

https://es.wikipedia.org/wiki/Altimetr%C3%ADa
https://www.aristasur.com/contenido/que-son-las-curvas-de-nivel-en-un-mapa-topografico
https://es.wikipedia.org/wiki/Curva_de_nivel

TEMA 3: MEDIDA DE ÁNGULOS Y DIRECCIONES

ÁNGULOS Y DIRECCIONES

Una de las finalidades de la topografía es la localización de puntos sobre la superficie terrestre, lo cual se logra si se conocen:

• La dirección y la distancia a partir de un punto conocido.
• La dirección desde dos puntos cocidos.
• La distancia distancia desde puntos conocidos conocidos.
• La dirección desde un punto y la distancia desde otro punto ambos igualmente conocidos otro punto, ambos igualmente conocidos.

1. Ángulo horizontal: Es aquel ángulo cuyos lados se encuentran encuentran sobre un plano horizontal horizontal.
2. Dirección de una línea: Es el ángulo horizontal que hay entre una línea y otra que se toma como referencia.
3. Ángulo vertical: Es aquel ángulo cuyos lados se encuentran sobre un plano vertical.
4. Pendiente de una línea: Es aquel ángulo vertical, de elevación o de depresión que hace una línea con la horizontal.

FORMA DE MEDICIÓN DE LA DIRECCIÓN DE UNA LÍNEA DIRECCIÓN DE UNA LÍNEA

De acuerdo a lo anterior las direcciones entre rectas que unen puntos sobre el terreno se pueden obtener de varias formas:

1. Midiendo los ángulos que hay entre rectas adyacentes.
2. Midiendo entre rectas no adyacentes sumando los ángulos que intervienen.
3. Midiendo el ángulo que hay desde una línea que se toma como referencia

CLASES DE MERIDIANOS:

Meridiano Verdadero o geográfico:

Es la recta imaginaria que une los polos geográficos Norte y Sur, los cuales son determinados por medio de observaciones astronómicas y donde para cada punto localizado localizado sobre la superficie superficie terrestre terrestre tiene siempre siempre la misma dirección. Esta línea imaginaria es utilizada como referencia para realizar la ubicación de cualquier línea que se encuentre sobre la superficie de la tierra.

Meridiano Magnético:

Es la línea imaginaria que une los polos magnéticos de la tierra Norte y Sur, los cuales se determinan por medio de la brújula, no son paralelos a los meridianos verdaderos, pues los polos magnéticos se encuentran encuentran separados separados de los polos geográficos. No poseen una dirección definida, pues los polos magnéticos están en constante movimiento. Esta línea imaginaria también es utilizada como referencia para realizar la ubicación de cualquier línea que se encuentre sobre la superficie de la tierra que se encuentre sobre la superficie de la tierra.

Meridiano Arbitrario:

Es una recta imaginaria, que se toma de forma arbitraria, arbitraria, a partir de la cual se inicia la lectura de los ángulos requeridos para la localización de un punto o para la realización de un levantamiento topográfico. Es de mucha utilidad en levantamientos en los cuales no se conoce la dirección de los meridianos geográficos o magnéticos, pero en donde su determinación es indispensable para la ubicación del objeto levantado dentro de un plano objeto levantado, dentro de un plano.

RUMBO

1. El rumbo de una recta es la dirección que ésta tiene con respecto al meridiano que se ha escogido como referencia.
2. El rumbo se indica por medio de un ángulo agudo (0° a 90°) que la recta hace con respecto respecto al meridiano escogido, a partir de los extremos Norte o Sur de dicho meridiano, teniendo presente de especificar el cuadrante  donde se encuentra la línea.
3. De acuerdo a lo anterior y dependiendo del meridiano que se halla tomado como referencia el rumbo puede  que se halla tomado como referencia, el rumbo puede ser, verdadero, magnético o arbitrario.

CONTRA-RUMBO

1. El contra-rumbo de la línea AB, es igual al rumbo de la línea AB mas 180°; o lo que el lo mismo, el rumbo de la línea BA.
2. El contra-rumbo posee el mismo valor en magnitud del ángulo que el rumbo, pero la diferencia primordial entre ambos, radica en que cambia la ubicación del cuadrante al cual pertenece la línea.
3. El contra-rumbo varia de 0° a 90°

AZIMUT

1. Azimut de una línea, es la dirección que esta hace con respecto al meridiano que se ha tomado como referencia; medido como el ángulo que existe entre el extremo extremo Norte del meridiano y la línea; varia de 0° a 360°.
2. Para medir el azimut de una línea, se toma la parte Norte del meridiano de referencia, en el punto de inicio del meridiano y se barre el ángulo en el sentido de las manecillas del reloj, hasta encontrar la línea a la que se le quiere encontrar el azimut.
3. El azimut puede ser verdadero, magnético o arbitrario; según el meridiano que se ha tomado como referencia según el meridiano que se ha tomado como referencia.

CONTRA-AZIMUT

1. El contra-azimut de la línea AB, es igual azimut de la línea AB mas 180°; o lo que el lo mismo, el azimut de la línea BA.
2. El contra-azimut se mide de 0° a 360°

DECLINACIÓN MAGNÉTICA:

La declinación magnética en un punto de la Tierra es el ángulo comprendido entre el norte magnético local y el norte verdadero (o norte geográfico). En otras palabras, es la diferencia entre el norte geográfico y el indicado por una brújula (el denominado también norte magnético).

Por convención, a la declinación se le considera de valor positivo si el norte magnético se encuentra al este del norte verdadero, y negativa si se ubica al oeste.

La expresión variación magnética equivale a declinación (magnética). Se emplea en algunas modalidades de navegación, entre ellas la aeronáutica. Las líneas de igual valor de declinación magnética se denominan curvas isogónicas (de igual valor angular).

De ellas, a las de valor nulo se les denomina curvas agónicas (sin ángulo). Una brújula ubicada en una posición representada en una curva agónica apunta exactamente al norte verdadero, ya que su declinación magnética es nula.

BIBLIOGRÁFICA:

• https://agroietal3.wordpress.com/angulos-y-direcciones/
• https://es.wikipedia.org/wiki/Declinaci%C3%B3n_magn%C3%A9tica

TEMA 2: MEDICIÓN DE DISTANCIAS DIRECTAS

1) Métodos de medición directa, equipo requerido para mediciones con cinta métrica  

La medida o medición diremos que es directa, cuando disponemos de un instrumento de medida que la obtiene comparando la variable a medir con una de la misma naturaleza física. Así, si deseamos medir la longitud de un objeto, se puede usar un calibrador. Observe que se compara la longitud del objeto con la longitud del patrón marcado en el calibrador, haciéndose la comparación distancia-distancia. También, se da el caso con la medición de la frecuencia de un ventilador con un estrobos copio, la medición es frecuencia del ventilador (nº de vueltas por tiempo) frente a la frecuencia del estrobos copio (nº de destellos por tiempo).

EQUIPO TOPOGRÁFICO PARA MEDIR DISTANCIAS

En topografía disponemos de un gran número de herramientas que forman parte de equipo para hacer mediciones. En esta ocasión, vamos a hablar sobre el equipo topográfico para medir distancias.

Dentro del equipo topográfico para medir distancias que se utilizan en topografía encontramos la cinta métrica, el odómetro y el distanciómetro.

CINTA MÉTRICA DENTRO DEL EQUIPO TOPOGRÁFICO PARA MEDIR DISTANCIAS

Antiguamente las cintas métricas eran simplemente unas telas de tramado resistente y enrolladas manualmente que se guardaban en recipientes forrados de cuero y con mecanismos de bronce.

Con el paso del tiempo los materiales fueron cambiando para mejorar la precisión de las medidas. En la actualidad, existen cintas métricas de fibra de vidrio para topografía y batimetría, cintas métricas de acero con revestimiento de nylon, cintas métricas de fibra de vidrio con revestimiento de PVC y las cintas métricas digitales.

Las cintas métricas permiten realizar levantamientos topográficos preliminares del terreno, esto se utiliza para conocer el terreno antes de realizar cualquier otra tarea.

El método de medir la distancia horizontal entre dos puntos con la cinta métrica se le llama cadenamiento. Además, existen cintas de diferentes materiales y longitudes.

ODÓMETRO DENTRO DEL EQUIPO TOPOGRÁFICO PARA MEDIR DISTANCIAS

El odómetro también llamado rueda de medición, los más utilizados poseen una sola rueda, aunque también los hay con dos.

La función del odómetro en topografía se complementa con las cintas métricas, distanciómetros u otro tipo de instrumentos de medición. Por lo tanto, el odómetro consiste en la medición de las distancias recorridas, de esta forma se mede la distancia exacta cuando se recorre una zona.

Existen odómetros mecánicos y electrónicos, y es muy útil para medir la distancia entre dos puntos. Aunque también se puede utilizar para medir áreas cuadradas o rectangulares, triangulares y en superficies irregulares.

DISTANCIÓMETRO DENTRO DEL EQUIPO TOPOGRÁFICO PARA MEDIR DISTANCIAS

Al distanciómetro también se le conoce como medidor láser, y consiste en la medición de dos puntos a través del láser. También se pueden encontrar distanciómetros sónicos, el cual mide la distancia con un método de ultrasonidos.

En topografía el que más se utiliza es el medidor láser, con este método se pueden medir distancias inclinadas desde un punto conocido a otro desconocido. A través del distanciómetro se pueden obtener, a través de cálculos, el nuevo punto y la cota.

Encontramos dos tipos de distanciómetro dentro del equipo topográfico para medir distancias:

Montura en horquilla: Es el que se monta sobre la horquilla del teodolito o tránsito. Este tipo de distanciómetro es más lento ya que primero apunta el telescopio y tras él, el distanciómetro.

Montura en telescopio: Ofrece mayor facilidad y rapidez, ya que, a diferencia de la montura de horquilla, únicamente apunta el telescopio un poco por debajo del prisma para realizar la medición. Es una montura de mayor especialización.

En muchas ocasiones se puede desajustar y la puntería para la medición de distancias a veces da problemas. A pesar de ello, el alcance de este tipo de equipos puede llegar hasta los 5 kilómetros, aunque existen distanciómetros manuales especializados en recintos y distancias cortas con mediciones de aproximadamente 200 metros.

ESTACIONES DENTRO DEL EQUIPO TOPOGRÁFICO PARA MEDIR DISTANCIAS

Otro del equipo necesario para la medición de distancias, pero también de ángulos, encontramos las estaciones. Las estaciones hay de muchas clases, por ejemplo, las hay motorizadas, sin prisma, con cálculo de coordenadas, con memoria… Y encontramos dos tipos de estaciones:

Estación Semitotal: En el cual se integra el teodolito óptico y el distanciómetro. Al tener ambos integrados, se trabaja más rápido que si montamos ambos por separado. Tiene lecturas analógicas, por esa razón es más recomendable una Estación Total. Se trata de un equipo topográfico para medir distancias y ángulos muy útil para medir replanteos de precisión y controles de obras.

Estación Total: En este tipo de estación se integra el teodolito electrónico, el distanciómetro y un ordenador. Hay muchas clases de estaciones totales y lo que más destaca de este tipo de estación es la precisión, el número de aumentos en la lente del objetivo, el compensador electrónico, el alcance y la memoria.

2) Mediciones en hechos físicos consolidados.  

Espacio y tiempo

En astrofísica, la medición del espacio y el tiempo resulta primordial como base de referencia para hacer cálculos de importancia. De hecho, ambas magnitudes están estrechamente ligadas desde la implantación del "año luz", como dimensión espacial. En 1976 se determinó un sistema internacional de constantes astronómicas (IAU) como marco de referencia común. Estas son algunas magnitudes de uso común en astrofísica:

MEDICION	MAGNITUD	DEFINICIÓN	Abrev.	VALOR
TIEMPO	SEGUNDO	Duración basada en cierto tiempo atómico	s	1 s
	DÍA	duración media de un día terrestre	D	86.400 s.
DISTANCIA	UNIDAD ASTRONÓMICA	Distancia media de la Tierra al Sol	UA	149.597.870 km
	AÑO LUZ	Distancia que recorre la luz en un año terrestre	ly	9,46728 × 1012 km
	PARSEC	Distancia en la que el paralaje de un astro ocupa 1 segundo de arco	pc	3,2616 ly

 La ciencia que estudia la ubicación de los astros en el firmamento y todo lo relacionado con distancias y posiciones, se denomina Astronomía de posición o Astrometría. En astronomía moderna, una vez resueltos los problemas que en la antigüedad planteaban los "tamaños", el dato más interesante es el de la distancia existente entre los cuerpos astrales.

Para calcular distancias, se utiliza entre otros sistemas, el paralaje, técnica de geometría aplicada que consiste en calcular proporciones partiendo de distancias ya conocidas, similar a una triangulación. Se aprovecha la diferencia de posición del observador en la Tierra a lo largo de medio año, consiguiendo así dos puntos de vista situados a 2 UA de distancia, desde los cuales se pueden observar dos posiciones subjetivas de un objeto lejano, lo que nos permitirá finalmente calcular distancias aproximadas (Ver Gráficos 1 y 2).

Para la triangulación (ver Gráfico 2) se utiliza el ángulo Tierra/Estrella/Sol, llamado "paralaje" ("p"), siendo "rs" la distancia Sol/Tierra y "r", la distancia a calcular. Dado que "rs" es mucho menor que "r", el ángulo "p"  (en radianes) es muy pequeño, por lo que su tangente es casi igual a él, con lo que la fórmula es similar a  p=rs/r donde conocemos que "rs" es 1 UA. Este método permite calcular distancias inferiores a 100 parsecs.

Para calcular distancias mayores, también puede usarse el método de las "cefeidas", estrellas muy brillantes cuyos períodos de oscilación de sus radios son bien conocidos, así como la relación que guardan entre su período, color y su luminosidad, aplicándose la fórmula:

 Mv= C1 + C2 lgP + C3 (B-V)

Siendo Mv = luminosidad absoluta en "v", P= período y C1, C2 y C3, constantes conocidas.

Finalmente, otros métodos utilizados son "la relación Tully-Fisher", que correlaciona la luminosidad absoluta con la anchura en 21 cm del espectro de radio de una galaxia espiral, bajo la fórmula  M= C1 lg (W/sen i) + C2  , así como la Ley de Hubble, que calcula la distancia relacionándola con la velocidad a la que se aleja una galaxia.

3) Mediciones en terreno horizontal, inclinado e irregular   

Es necesario que la cinta siempre esté en un posición horizontal. Entonces se usa la plomada para proyectar el cero o el extremo de la cinta sobre el punto donde debe ir el piquete. Cuando no se requiere demasiada precisión basta con un jalón, en vez de plomada, cuidando que éste permanezca vertical. Que la cinta debe estar muy templada para evitar que se forme una catenaria. Cuando el terreno es demasiado inclinado, como lo muestra la figura, se mide por partes,tomando tramos tan largos como sea posible, manteniendo la cinta horizontal El procedimiento es básicamente igual al utilizado en la medición en terreno plano, con la diferencia que en cada cinta da se debe garantizar que la cinta esté lo más horizontal posible, para ello es recomendable llevar un nivel de mano,pues a simple ojo se cometen errores de apreciación en la horizontalidad.

4) Errores en la medida de distancias y sus tolerancias permisibles  

La tolerancia es la cantidad máxima de error que se puede cometer en la realización de un trabajo topográfico.El punto más desfavorable del trabajo no debe ser peor que el valor de la tolerancia.La tolerancia está directamente relacionada con el límite de percepción visual, ya que suelen igualarse. La tolerancia va a ser la que nos plantee el trabajo, según la cual se decidirá el instrumental a utilizar, el método de observación, la hora de la toma de datos y los métodos de cálculo de gabinete.Supongamos que nos encargan la realización de un mapa a escala 1/25.000, en el que la tolerancia es de 5 metros (límite de percepción visual). Cualquier detalle inferior a esta distancia no tendrá representación en el plano y por tanto no tendrá que tomarse. El instrumental topográfico no es necesario en este caso, que tenga una alta precisión y la compensación de los errores tampoco es necesario que disponga de un gran desarrollo matemático.Sin embargo si nos encargan realizar un plano a escala 1/500, cuya tolerancia sea 10 cms., ya hay que tomar todos los detalles mayores de 10 cms., y para ello utilizar un método de observación en el que se anulen o minimicen los errores para que sean inferiores a esa cantidad, y utilizar un aparato que asegure una precisión mejor.

5) Calculo de Áreas simples, por formulas trigonométricas y método de Heron

Triángulo de lados a, b, c.

En geometría plana elemental la fórmula de Herón, cuya invención se atribuye al matemático griego Herón de Alejandría,¹​ da el área de un triángulo conociendo las longitudes de sus tres lados a, b y c:

${\displaystyle {\acute {A}}rea={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}}$

donde s es el semiperímetro del triángulo:

${\displaystyle s={\frac {a+b+c}{2}}}$.

Cualquier polígono simple puede ser separado en triángulos que a lo más tienen un lado común o un vértice común, mediante diagonales que parten de un único vértice apropiado. Esta subdivisión y la aplicación de la norma herodiana para el área triangular, facilita el cálculo del área de la región plana encerrada por el polígono simple, con solo medir longitudes, allí radica su importancia.

La fórmula también puede expresarse de estas otras formas:

${\displaystyle {\acute {A}}rea={\ {\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\ \over 16}}\,}}$

${\displaystyle {\acute {A}}rea={\ {\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})\ \over 16}}\,}}$

${\displaystyle {\acute {A}}rea={\ {\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)\,}}\ \over 4}\,}$

${\displaystyle {\acute {A}}rea={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}.}$

La fórmula de Herón se distingue de otras fórmulas para hallar el área de un triángulo, como la de la mitad de la base por la altura o la de la mitad del módulo de un producto cruz de dos lados, por no requerir ninguna elección arbitraria de un lado como base o un vértice como origen.

BIBLIOGRÁFICA:

• http://aprendefisika.blogspot.com/p/metodo-directo-e-indirecto.html
• http://www.globalmediterranea.es/equipo-topografico-medir-distancias/
• https://sites.google.com/site/canaldeciencias/astrofisica/fenomenos-y-medicion
• https://www.coursehero.com/file/p17h1va/Medici%C3%B3n-en-un-terreno-inclinado-o-irregular-Es-necesario-que-la-cinta-siempre/
• https://es.scribd.com/doc/59150826/Tolerancias-en-Nivelación-y-Planetaria

VERNIER

HISTORIA DEL VERNIER

El Vernier es un instrumento  llamado también “Calibre deslizante o pie de rey”.  Su nombre viene del apellido del matemático francés Pierre Vernier (1580-1637) quien adapto la idea de Pedro Nunes (Petrus Nonius 1492-1577) a  la medición lineal . Nunes invento este aparato y lo aplico al esferómetro.  Pedro Nunes, conocido también por su nombre latino como Petrus Nonius (Alcácer do Sal, Portugal, 1492 - Coímbra, 1577), matemático, astrónomo y geógrafo portugués, del siglo XVI. Inventó en 1514 el nonio, un dispositivo de medida de longitudes que permitía, con la ayuda de un astrolabio, medir fracciones de grado de ángulos, no indicadas en la escala de los instrumentos. Pierre Vernier (Ornans, 1580 - Ornans, 1637) matemático francés, es conocido por la invención en 1631 de la escala vernier para medir longitudes con gran precisión y basado en el de Pedro Nunes.Dada la primera invención de Pedro Nunes (1514) y el posterior desarrollo de Pierre Vernier (1631), en la actualidad esta escala se suele denominar como nonio o vernier, siendo empleado uno u otro termino en distintos ambientes, en la rama técnica industrial suele ser mas utilizado nonio.

VERNIER

El vernier es un instrumento constituido por un par de reglas, una fija y una deslizante, y unos topes que facilitan la medida de dimensiones exteriores, dimensiones interiores y profundidades de objetos. Usualmente la reglilla móvil (nonio) tiene marcada diez divisiones que abarcan nueve divisiones de la regla fija (principal), de manera que cada división del nonio corresponde a 9/10 de una división de la regla principal.

Llamado también calibre deslizante o pie de rey es el instrumento de medida lineal que más se utiliza en el taller. Por medio del Vernier se pueden controlar medidas de longitud internas, externas y de profundidad. Pueden venir en apreciaciones de 1/20, 1/50 y 1/100 mm y 1/128 pulg, es decir, las graduaciones al igual que la regla graduada vienen en los dos sistemas de unidades en la parte frontal.

En algunos instrumentos en el reverso se encuentran impresas algunas tablas de utilidad práctica en el taller, como la medida del diámetro del agujero para roscar.

El material con que se construyen es generalmente acero inoxidable INVAR., que posee una gran resistencia a la deformabilidad y al desgaste.

EL NONIO:

Representa la característica principal del vernier, ya que es el que efectúa medidas con aproximaciones inferiores al milímetro y al 1/16 de pulgada. La graduación señalada en el cuerpo del calibre, y entre marcas, representa un milímetro, como si se tratara de una regla normal.

La graduación del nonio en milímetros posee 20 divisiones si se trata de un instrumento con apreciación de 0.05 mm, en este caso sólo podemos efectuar mediciones en múltiplos de 5 centécimas de milímetro.

Cuando el 0 del nonio coincide con el 0 de la escala del cuerpo, el vernier está cerrado. En esta posición la vigésima marca del nonio coincide con la posición de 39 mm de la escala fija. Ningún otra marca del nonio, comprendida entre el 0 y el 10, coincide con un marca de la escala del cuerpo del calibre.

Si abrimos la corredera de modo que la primera marca del nonio después del cero (entre 0 y 1 mm) coincida con la segunda marca de la escala fija del cuerpo, la medida será 0.05 mm. Si actuamos nuevamente y hacemos coincidir la segunda marca, la medida será ahora 0.10 mm.

CALIBRADOR VERNIER

La  escala vernier lo invento Petrus nonius matemático portugués por lo que se le denomina nonius. El diseño actual de  escala deslizante debe su nombre al francés Pierre vernier quien lo perfecciono. El calibrador vernier fue elaborado para satisfacer s necesidades de un instrumento de lectura directa que pudiera brindar una medida fácilmente, en una solo operación el calibrador típico puede tomar tres tipos de medición exteriores, interiores y profundidades, pero algunos pueden tomar medición de peldaños.

 Es un instrumento para medir longitudes que permite lecturas en milímetros y en fracciones de pulgada, a través de una escala llamada Nonio o Vernier.

Está compuesto por una regla fija que es donde están graduadas las escalas de medición ya sea en milímetros, en pulgadas o mixtas.

Las partes del pie de metro son:

Regla: Graduada en los sistemas métrico e inglés.

• Pata fija: Con superficie de contacto a la pieza para medir exteriormente.
• Pata móvil: Con superficie de contacto móvil a la pieza para medir exteriormente.
• Punta fija: Parte fija de contacto con la pieza, para medir interiormente.
• Punta móvil: Parte móvil de contacto con la pieza para medir interiormente.
• Impulsor: Apoyo del dedo pulgar para desplazar el cursor.
• Tornillo de fijación o freno: Fija la medida obtenida actuando sobre la lámina de ajuste.
• Nonio: Escala que otorga la precisión del instrumento según su cantidad de divisiones.
• Reglilla de profundidad: Está unida al cursor y sirve para tomar medidas de profundidad.

BIBLIOGRÁFICA:

https://todoingenieriaindustrial.wordpress.com/metrologia-y-normalizacion/calibrador-vernier/

https://verniersecciona.wordpress.com/2008/04/13/definicion-de-vernier-o-pie-de-rey/

https://es.wikipedia.org/wiki/Calibre_(instrumento)